3. Solving free boundary systems by using neural networks
In a series of work, we developed some novel numerical schemes based on neural networks to solve different free boundary problems and proved the convergence of the schemes theoretically.
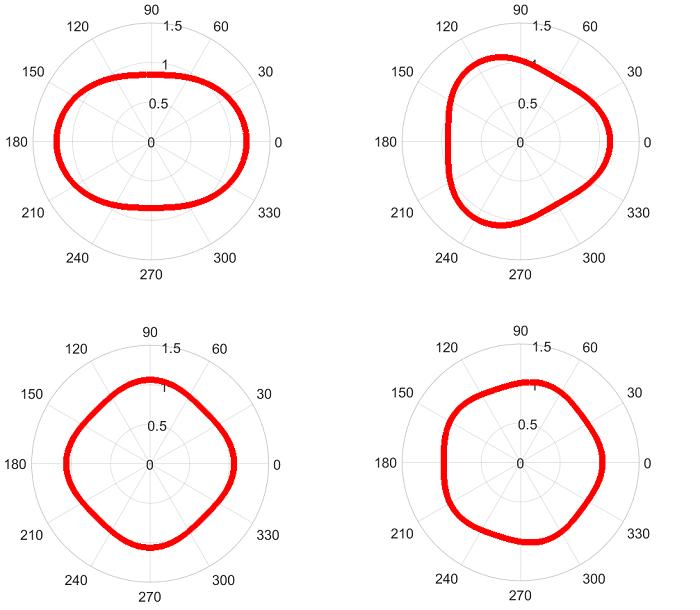
In one project, we proposed a method based on boundary integral method and neural network discretization to solve a modified Hele-Shaw problem with surface tension. In the simulations, we first verified this approach on radially symmetric and known non-radially symmetric solutions. The following 4 figures show the shapes of symmetry-breaking solutions on n=2, n=3, n=4, and n=5 bifurcation branches. All these solutions can be fully characterized by the theoretical bifurcation analysis and are recovered by our numerical method.
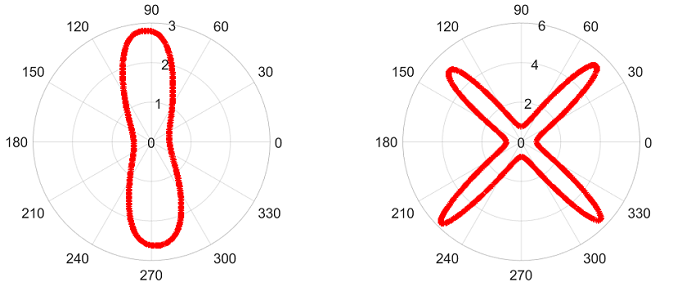
Moreover, we further verified the capacity of the new method by computing some non-radially symmetric solutions which are not characterized by any existing theories. In particular, we found the following fingering-like patterns.
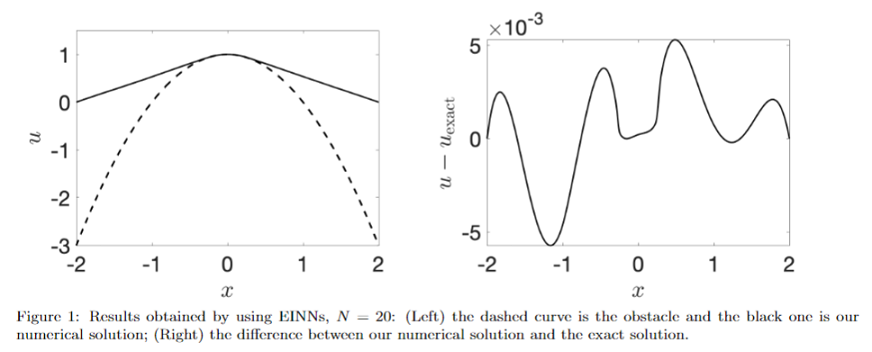
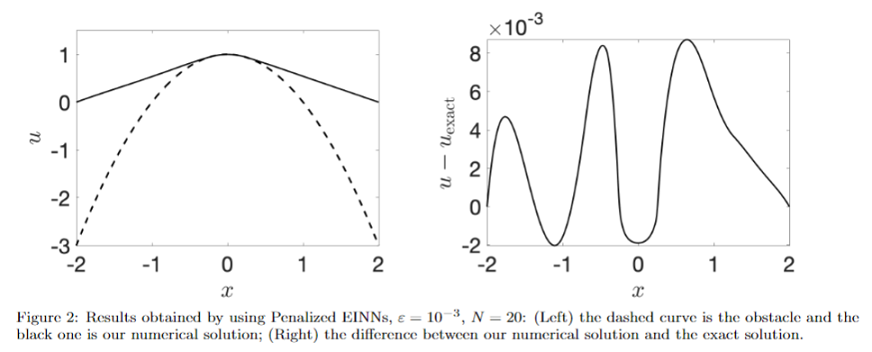
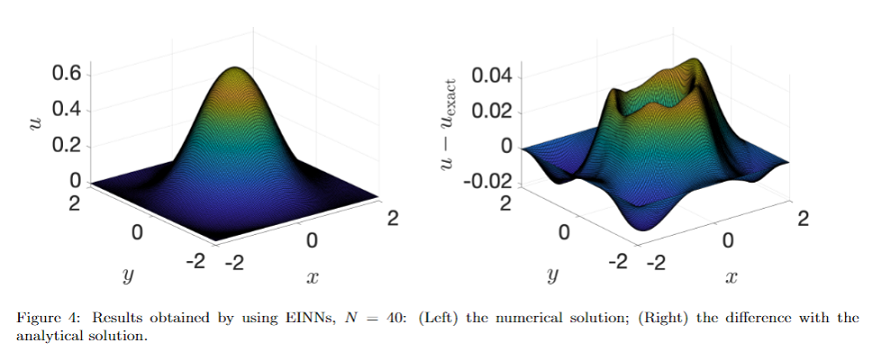
In another projection, we proposed two neural-network-based numerical schemes to solve the elliptic obstacle problems. In the first method, energy informed neural networks (EINNs), the cost function comes naturally from the energy minimization of the problem. As for the second method, Penalized EINNs, we took the variation form of a penalized system as the cost function. We rigorously proved the convergence of the two schemes and derive the convergence rates with the number of neurons N . In the simulations, we used two example problems (both 1-D and 2-D) to verify the convergence rate of the methods and the quality of the results.
Journal papers
-
X. E. Zhao, W. Hao and B. Hu, “Convergence analysis of neural networks for solving a free boundary problem”, Computers & Mathematics with Applications, 2021. [ DOI | arxiv ]
-
X. E. Zhao, W. Hao and B. Hu, “Two neural-network-based methods for solving elliptic obstacle problems”, Chaos, Solitons and Fractals, 2022. [ DOI | arxiv ]
Presentations
- “Two neural-network-based methods for solving elliptic obstacle problems”, AMS Fall Central Sectional Meeting, El Paso, 2022. [ slides ]
Posters
- X. E. Zhao, W. Hao and B. HU, “Solving a Free Boundary System by Using Neural Networks”. [ poster ]