4. A nonlinear cell-cell adhesion model
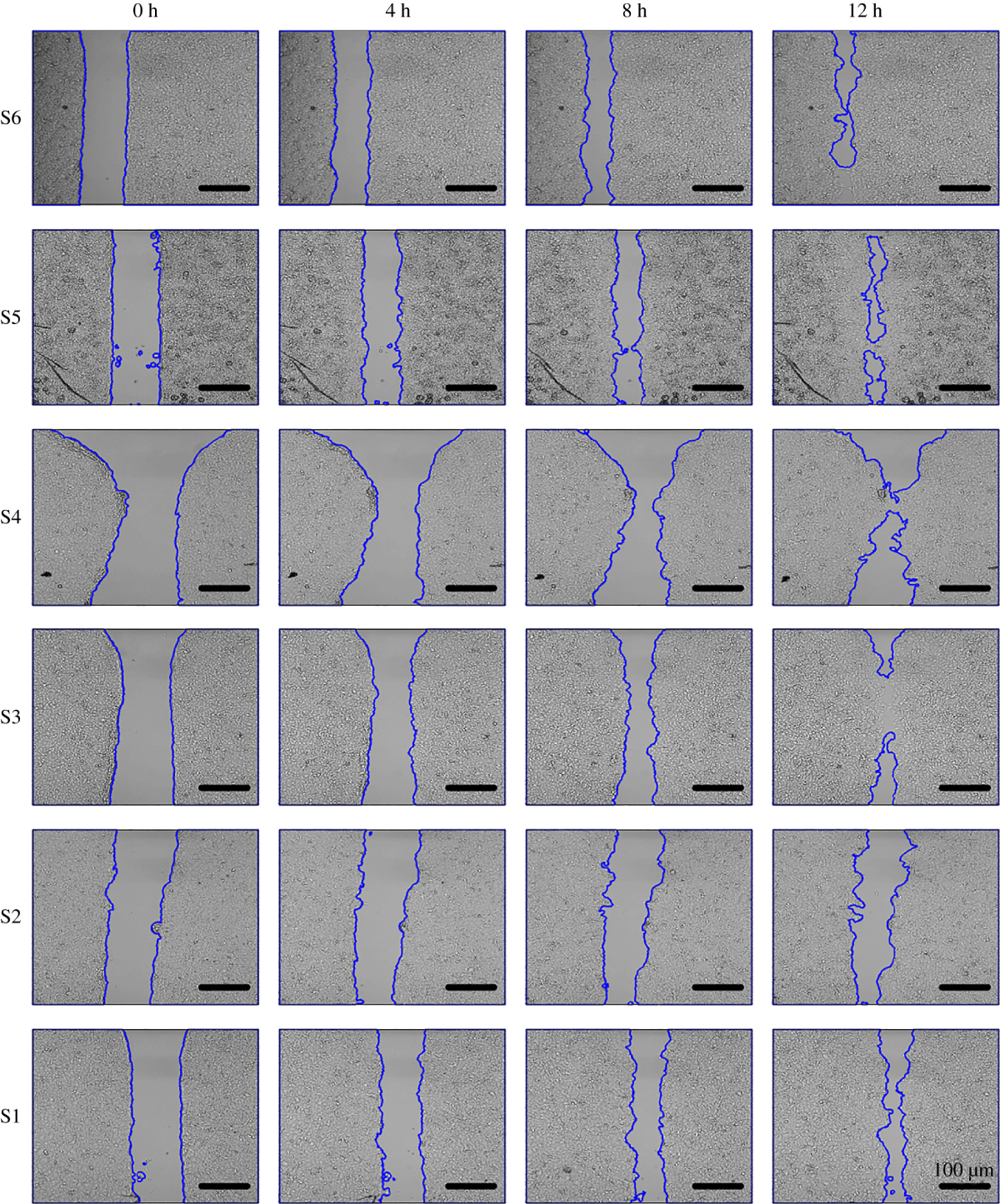
A nonlinear partial differential equation containing a nonlocal advection term and a diffusion term is analyzed to study wound closure outcomes in wound healing experiments. A wound healing experiment is done by making a scratch on a cell monolayer and capturing images at regular time intervals (Figure above: Images of wound healing assays from six experimental cell groups, Bobadill et. al., 2019, J R Soc Interface). There can be different outcomes for these experiments. Even though they all start from almost uniformly-wound edges, some result in relatively uniform wound closure (for example, S1), while in other cases, the leading edges are nonuniform (for example, S3). In order to explain different wound healing outcomes, we considered a nonlocal PDE and carried out bifurcation and stability analysis. Our analysis shows that higher cell-cell adhesion force corresponds to nonuniform edges in wound closure.
Journal papers
- G. Webb and X. E. Zhao, Bifurcation analysis of critical values for wound closure outcomes in wound healing experiments, Journal of Mathematical Biology. [ DOI ]
Presentations
- Bifurcation Analysis of Critical Values for Wound Closure Outcomes in Wound Healing Experiments, ICMA-VIII, Lafayette, 2022. [ slides ]
- Bifurcation Analysis of Critical Values for Wound Closure Outcomes in Wound Healing Experiments, JMM, Boston, 2023. [ slides ]
- Bifurcation Analysis of Critical Values for Wound Closure Outcomes in Wound Healing Experiments, 2023 Shanks Workshop, Nashville, 2023. [ slides ]
- Bifurcation Analysis of Critical Values for Wound Closure Outcomes in Wound Healing Experiments, DSLS 2023, Columbus, 2023. [ slides ]
Posters
- G. Webb and X. E. Zhao, Bifurcation Analysis of Critical Values for Wound Closure Outcomes in Wound Healing Experiments. [ poster ]